2013年度開成高校入試問題数学大問4を大人の力で解く（Python）

こんにちは、ぱそきいろです。

youtube見ていたら、面白そうな問題が出てきました。
開成高校の入試問題なのですが、こんな問題中学生が解けるのか・・・
（今でも解けなかった。。。）
www.youtube.com
悔しいので大人の力（プログラム）で解いていきます。

問題
感想
方針
コード
結果
まとめ

問題

開成高校2013年数学大問4

3つの自然数p,q,rは、1 ≦ p < q < r ≦ 6を満たす。
立方体のサイコロがあり、各面にp,q,rのいずれか一つが書かれている。
p,q,rの書かれた面はいずれも1面以上ある。
このサイコロを振って、出た目の合計を得点とするゲームを行う。
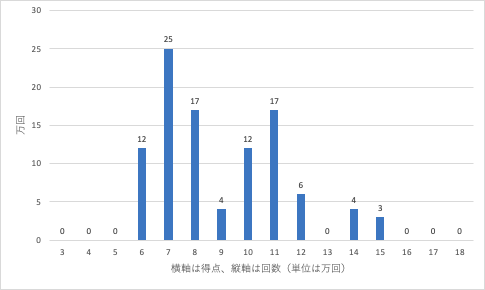
このゲームを100満開行った後、獲得点が出た回数をグラフにしてまとめたところ、結果は以下のグラフになった。
なお、各得点の回数は千の位の数を四捨五入した。
このとき、以下の問いに答えよ。
(1) p,q,rを求め、結果のみを答えよ。
(2) p,q,rが書かれた面の数は、それぞれ幾つであると考えられるか。そのように考えた理由も記せ。
なお、サイコロの6つの各面が出る確率は同様に確からしいとする。

感想

詳しい解説は冒頭のyoutubeを見てください。
私は真っ先にp=2、q=5と決めてしまい、引っかかりました。
ポイントは「各得点の回数は千の位の数を四捨五入した」ですね。
これによってq=6があり得るんですね、、、
ちなみにこれを15分で解く中学生とかおるのかよ。。。

方針

簡単な方針としては、

0~6^6までの6進数を生成する
生成した6進数に111111を足す（これをサイコロの目とする）
サイコロの目の数字の種類が3つであることを確認する
とりあえず100回ゲームをして、グラフの数字が出るかを確認する
出そうだったら10万回ゲームをして得点を調べる
「結果の分布の回数」と「問題の得点分布の回数」をそれぞれ二乗誤差をとって最も少ないものを答えとする（0になったらその時点で答えとする）

こんなところで調べてみます。
4.でとりあえず100回投げるのは計算量を減らすためです。
かつ、100万回のところを10万回にしています。
さすがに大きな偏りは出ないだろうと思ってます。

コード

まずはメインのループです。

    for i in range(6**6):
        #6進数に変換する
        dice=str(Base_10_to_n(i,6))
        
        #サイコロの目が3種類かを確認する
        c=collections.Counter(dice)
        if len(c.keys())!=3:
            continue
        #とりあえず100回投げてみる
        if test100throw(dice):
            #正しそうなら、10万回投げてみる
            pointlist=mainthrow(dice)
            #結果の得点リストを問題文の得点リストと比較して最小を更新するならprintする
            if judgepointlist(pointlist)<minscore:
                minscore=judgepointlist(pointlist)
                mindice=dice
                print(dice)
                print(minscore)
            #二乗誤差が0ならそこで終了する
            if minscore==0:
                break

コメントで説明しています。
次にそれぞれの関数を載せておきます。
6進数の変換は以下を参考にしています。
Python で10進数とn進数の変換

#6進数に変換して、111111をプラスする
def Base_10_to_n(X, n):
    X_dumy = X
    out = ''
    while X_dumy > 0:
        out = str(X_dumy % n) + out
        X_dumy = int(X_dumy / n)
    if out=="":
        out=0
    return int(out)+111111

#サイコロを3回投げて獲得した得点を返す
def throwdice(dice):
    point=0
    for j in range(3):
        point+=int(dice[random.randint(0,5)])
    return point

#10万回ゲームを試す
def mainthrow(dice):
    pointlist=[0 for i in range(19)]
    for k in range(100000):
        pointlist[throwdice(dice)]+=1
    return pointlist

#100回ゲームをして、分布の数字が含まれるかを判定する
def test100throw(dice):
    testlist=[0 for i in range(19)]
    for l in range(1000):
        testlist[throwdice(dice)]+=1
    judge=1
    for m in [6,7,8,9,10,11,12,14,15]:
        judge*=testlist[m]
    if judge!=0:
        return True
    else:
        return False

#問題の分布との出現回数の二乗誤差をとる
def judgepointlist(pointlist):
    anslist={6:12,7:25,8:17,9:4,10:12,11:17,12:6,14:4,15:3}
    #print(pointlist)
    score=0
    for n in anslist.keys():
        score+=(round(pointlist[n]/1000)-anslist[n])**2

    return score

不明点等ありましたら、コメントに残していただければと思います。
これで一通り実装ができたので動かしていきたいと思います。

結果

サイコロの目と二乗誤差を交互に出しています。
ちょっと偏りが出て二乗誤差が2とか1になってますが、2が3つ、3が2つ、6が1つが正解になりそうです。
ということで、回答としては
(1) p=2,q=3,r=6
(2) p 3つ, q 2つ, r 1つ
ですね。
(1)は結果のみを答えよなので文句なしで特典ありますね笑

まとめ

100万回のところを10万回に省略したため、若干の誤差がありますが、答えは断定できましたね。
何回も言いますけど、これを解く中学生がいるのが信じられないです。。
また機会があれば入試問題をプログラミングで解いていきたいと思います。
ありがとうございました。

ぱそきいろのIT日記

ぱそきいろがITに関する記事を書いていきます。

2013年度開成高校入試問題数学大問4を大人の力で解く（Python）

問題

感想

方針

コード

結果

まとめ